[자료구조] 2.3 하노이 타워

하노이 타워

하노이 타워 (The Tower of Hanoi)

하노이 타워 문제

1. 기본적으로 3개의 원반이 존재한다
2. 원반의 크기는 작은 원반, 중간 원반, 큰 원반이 있다.
3. 기둥 3개 A, B, C 가 존재한다
4. A의 기둥에 무거운 순서대로 원반 3개가 꽂혀 있다
5. 문제 : 기둥 A의 원반들을 모두 기둥 C로 옮기려면 어떻게 해야 하는가?
   • 제약사항
   • 원반은 한번에 하나만 옮길 수 있다
   • 작은 원반 위에 큰 원반은 올릴 수는 없다

하노이 타워 문제 풀이

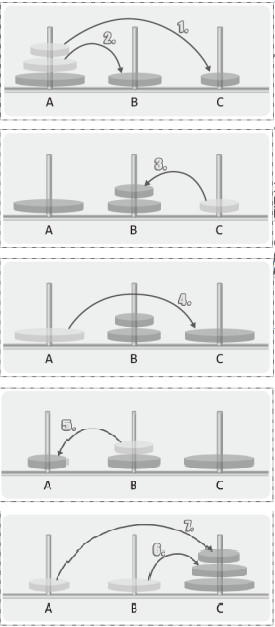
반복 패턴 연구

• 원반의 숫자가 많은 경우에도 풀이 패턴은 동일하다
• 4개의 원반인 경우
  1. 작은원반 3개를 A에서 B로 이동
  2. 큰 원반 1개를 A에서 C로 이동
  3. 작은 원반 3개를 같은 패턴으로 B에서 C로 이동

하노이 타워의 구현

void HanoiTowerMove(int num, char from, char by, char to) {
	if (num == 1) {
		printf("원반1을 %c에서 %c로 이동 \n", from, to);
	} else {
		HanoiTowerMove(num - 1, from, to, by);
		printf("원반%d을(를) %c에서 %c로 이동 \n", num, from, to);
		HanoiTowerMove(num - 1, by, from, to);
	}
}
int main(void) {
	HanoiTowerMove(3, 'A', 'B', 'C');
	return 0;
}

참고

• 윤성우의 열혈 자료구조
  
• 윤성우의 열혈 자료구조 강의